福晶科技：BBO晶体助力量子纠缠实验与量子科学发展

 

世界的本质居然真是量子化的，而上帝，真的是在掷骰子......

 

---

 

今年的诺贝尔物理学奖颁发给了用实验证实量子纠缠的三位科学家：约翰·克劳瑟（John Clauser）和阿兰·阿斯佩（Alain Aspect）以及安东·泽林格（Anton Zeilinger ），以表彰其“对纠缠光子进行的实验，建立了贝尔不等式（Bell inequalities）的违逆性和开创了量子信息科学”。如果爱因斯坦知道的话不知是否还会固执于自己的想法，认为“上帝不会掷骰子”，量子纠缠原本只是思维实验，如今被科学家用实验证实。

 

图1. 2022年诺贝尔奖得主

 

在EPR论文(1935)发表约30年后，J.S.Bell[1]于1964年关于Bell不等式的论文的发表，给出用定量的实验检验来判定这项物理学中重大哲学争论的可能性。经Clauser，Horne，Shimony和Holt[2](1969)，Clauser和Horne[3](1974)的努力后，人们终于有了能真正用于实际实验检验的两种不等式，即CHSH不等式和CH不等式。很显然，要完成对Bell不等式的实验检验，最重要的一项前提任务无疑是制备纠缠粒子对。

 

科学家们从1972到1982年共完成了12个实验，其中，10个实验的结果同量子力学预言一致而违反Bell不等式。诺奖得主A.Aspect于1982年完成的一个实验被称为反对定域实在论的“结论性证据”[4]。然而，由于定域实在论和量子力学之争的复杂性和重要性，以及Bell不等式实验检验本身还存在着不少“漏洞”，因此，物理学家们从未停止对Bell不等式检验的实验的研究，也在不断寻求新的更有效的制备纠缠光子对的方法。至今已完成了大量实验，而福晶科技的BBO非线性光学晶体对后续纠缠光子实验的发展和进步起到了重要作用，并凭借其优势逐渐成为制备纠缠光子的主要方法。

 

在1982年以前所完成的12个实验中，7个使用原子级联辐射光子对，4个使用湮灭辐射光子对，1个使用质子对。由于这几种源技术存在着自身固有的缺陷，例如随机延迟选择思想在原子级联发射光子源中难以实现，实验结构复杂，效率较低，稳定性较差，不易于分析。所以1988年以后完成的实验大多数采用一种被称为光学自发参量下转换(parametric down-conversion，PDC)的技术来产生纠缠光子对。一个光子通过自发参量下转换变为一对光子存在着两种方式，这取决于下转换光子对的两个光子是具有相同的偏振还是正交的偏振，这正是文献中常称它们为Ⅰ类（type-Ⅰ）参量下转换和Ⅱ类（type-Ⅱ）参量下转换的缘故。这种光子源有显著的优点，首先结构简单，易于实现，便于探测；其次能够产生非常细小的两个关联光子束，可以输入到很大长度的光纤中去或在自由空间中传输，因而光源和测量装置之间允许分开很远，目前已超过上千公里，使验证实验更加直接和客观。此后使用非线性光学晶体尤其是利用BBO晶体制备高亮度纠缠光子对的方法逐渐成为主流。

 

重要纠缠光子实验中BBO的身影

 

1979年中科院福建物质结构研究所陈创天教授团队发明了BBO非线性光学晶体，引起了国际光学界的极大兴趣。在1990年福建物构所成立福建晶体技术开发公司（福晶科技前身）之前，研究所就已经开始了BBO，LBO和KD*P等非线性光学晶体生产和对外销售。1988年，Shih和Alley[5]小组发表了“New Type of Einstein-Podolsky-Rosen-Bohm Experiment Using Pairs of Light Quanta Produced by Optical Parametric Down Conversion”一文，这是最早采用参量下转换技术和非线性光学晶体产生纠缠光子对进行Bell不等式检验的实验报道。实验使用的晶体是Ⅰ类相位匹配KD*P晶体（如图2）。实验数据为d=0.34±0.03，该实验结果展示了对Freedman不等式的3个标准偏差的违反。

 

此实验开启了非线性光学晶体制备纠缠光子的时代。此时，BBO晶体还只是作为输入光倍频晶体参与实验，由KD*P晶体产生纠缠光子。

 

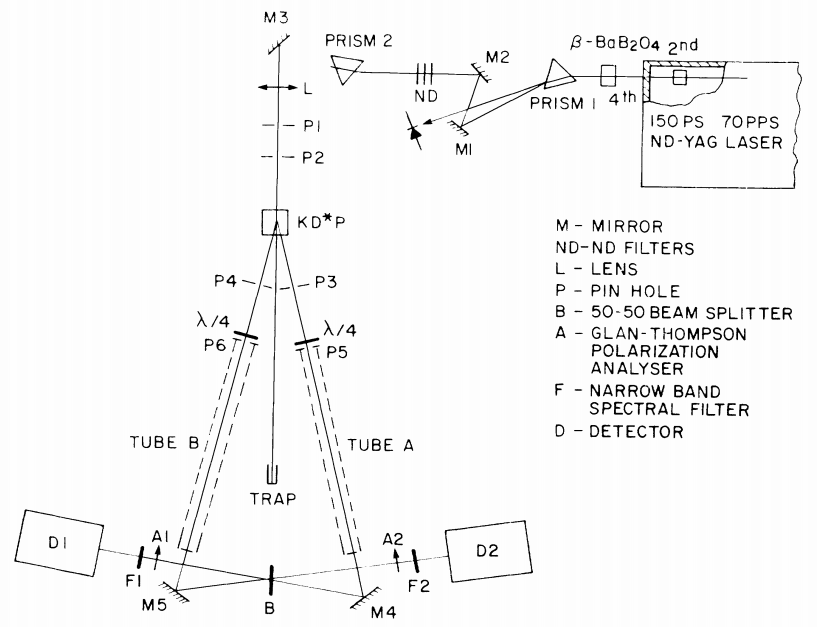
图2. 实验装置示意图[5]

 

1992年，Brendel，Mohler和Martiessen[6]发表了“Experimental Test of Bell’s Inequality for Energy and Time”一文，该报道是最早的直接使用BBO晶体制备纠缠光子对的实验之一，在一个特别简单且易于分析的结构中（如图3）对能量和时间的贝尔不等式进行了测试检验，而除了由Rarity和Tapster于1990年所完成的基于“相位和动量”的实验之外，以前所有的实验都是对于自旋或偏振的变量的检验。最终的实验结果获得了高达86%的最大可见性，并以7个标准偏差对能量和时间的Bell不等式的违反。

 

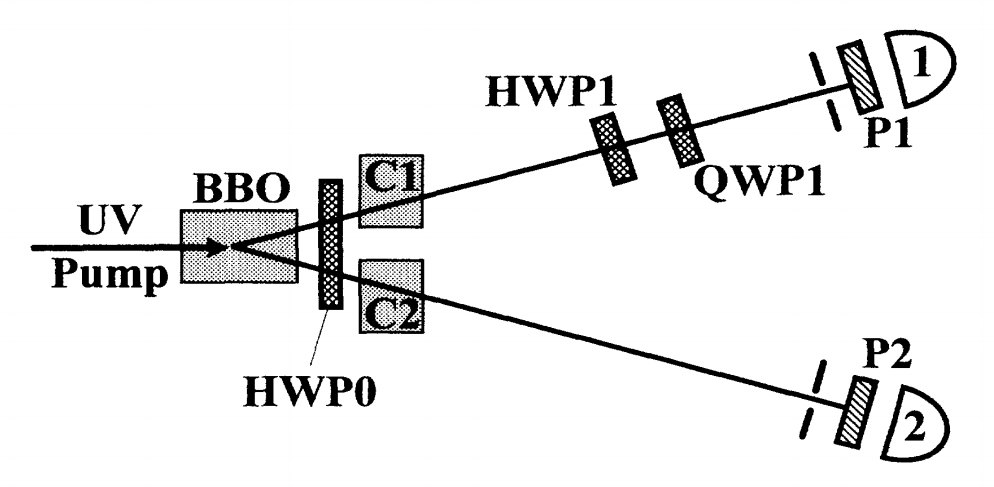
图3. 实验装置示意图[6]

 

1993年，Kiess，Shih，Sergienko和Alley[7]发表了“Einstein-Podolsky-Rosen-Bohm Experiment Using of Light Quanta Produced by Type-Ⅱ Parametric Down Conversion”一文，首次采用BBO晶体在Ⅱ类相位匹配的参量下转换中产生的纠缠光子对来检验Bell不等式。他们给出的实验数据是S=0.316±0.003，并在文中说明该实验以22个标准偏差违反Freedman不等式。

 

1995年，Kwiat，Mattle，Weinfurter和Zeilinger[8]发表了“New High Intensity Source of Polarization-Entangled Photon Pairs”一文。首次采用非共线Ⅱ类相位匹配技术来产生纠缠光子对进行Bell不等式检验实验，所需的偏振纠缠态光子直接从一个非线性光学晶体（使用的是BBO晶体）产生，不需要额外的分束器或镜子（如图4）。此实验的重要性在于它所提供的这种光源的亮度比以往的偏振纠缠光子源高一个数量级以上。作者们在文中指出，根据所获得的数据(-2.6489±0.0064)可知该实验在5分钟内获得的对CHSH不等式的违反大于100个标准偏差。此实验提出了一个更简单的依赖于非线性Ⅱ类相位匹配的技术方法。偏振纠缠态光子直接产生于单个非线性晶体（BBO），不需要额外的分束器或反射镜，也不需要丢弃检测到的光子对来观察非局域相关。

 

此前，大多数自发参数下转换光子的实验都采用Ⅰ类相位匹配，其中相关光子具有相同的偏振。在简并发射的情况下，一对波长相等的光子出现在以泵浦光为中心的锥上，锥的开口角取决于晶体光轴与泵浦光的夹角。通过Ⅱ型相位匹配，下转换的光子被发射到两个锥（如图5），一个是普通偏振，另一个是异常偏振。在共线情况下，两个锥恰好在一条线上相切共线，即泵浦光方向。在锥重叠的地方，光基本上可以呈现纠缠态。

 

图4. 一种从下转换晶体中产生和选择偏振纠缠态的方法示意图[8]

 

额外的双折射晶体Cl和C2，以及半波板HWPO，被用来补偿来自生产晶体的双折射步行效应。通过适当设置半波板HWP1和四分之一波板QWP1，可以产生所有四种正交EPR-Bell态。每个偏光片P1和P2由两个堆叠的偏光分束器组成，前有一个可旋转的半波片。

 

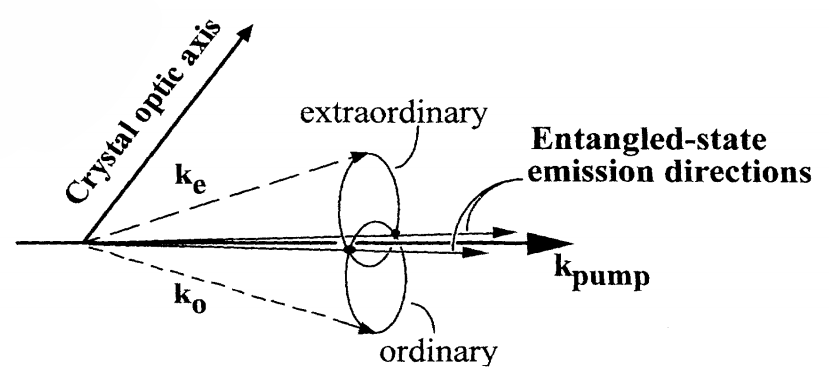
图5. Ⅱ型相位匹配下自发参量下转换锥，纠缠光子位于泵浦光的两侧[8]

 

此方案有许多明显的优势，由于结构简单，状态非常稳定，该方案比其他下转换设置能更快获得纠缠光子对，相位漂移对偏振纠缠态影响极小，明显优于动量纠缠态或能量-时间纠缠态。此外，还可以将偏振纠缠态转换为动量-能量-时间纠缠态。此技术方案能够应用于许多需要稳定的易于控制的两个粒子纠缠态源的实验中，特别是量子通信的实验，包括量子加密、隐形传态以及量子计算领域。此方案大大促进了这类实验，以及对量子力学基础的研究，甚至学生在实验室都能实现。 

 

1998年，Weihs，Jennewien，Simon，Weinfurter，和Zeilinger[9]发表了“Violation of Bell’s Inequality under Strict Einstein Locality Conditions”的论文。根据Ⅱ类参量下转换原理，选用BBO晶体产生偏振纠缠的光子对（如图6），此实验中分析器与检测器之间的距离是400m，测得偏振分析的选择方向和检测光子的总时间约为100ns，明显小于光传播这段距离所需的时间（1.3ms），符合爱因斯坦定域性条件的要求；每一个检测器对局部的线性偏振的分析方向都是由一个电子-光子的电压调节器所决定的；方向的选择是基于一个随机数发生器。实验最终数据是S=2.73±0.02，违反CHSH不等式超过30个标准偏差。这个实验的重要性在于被认为是力图超越1982年Aspect实验而又的确取得重大成就的第一个实验，因为它第一次真正严格地实施了爱因斯坦定域性条件，已经封闭了定域性漏洞。

 

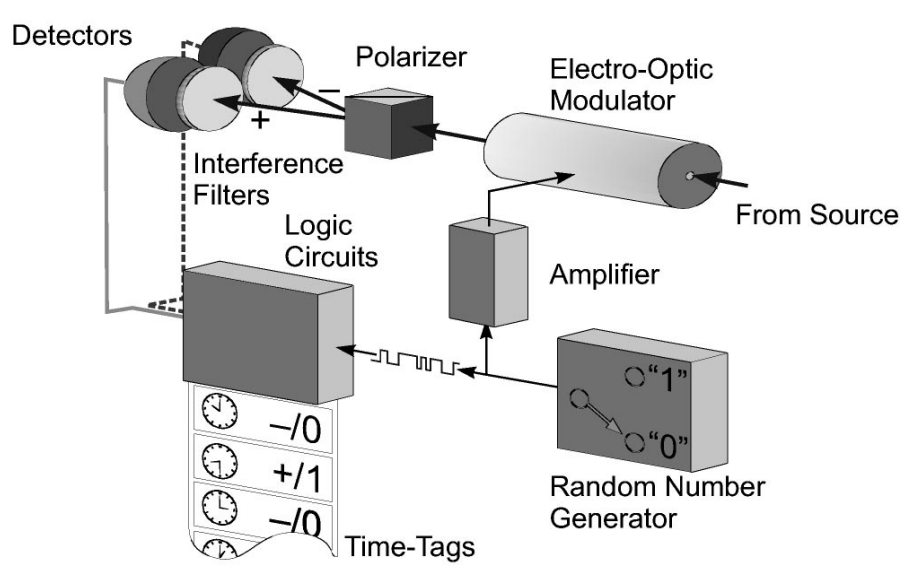
图6. 实验装置示意图

（Electro-Optic Modulator元器件为BBO晶体）[9]

 

1999年，Kwiat，Waks，White，Appelbaum和Eberhard[10]发表“Ultrabright Source of Polarization-Entangled Photons”一文，他们采用两块BBO晶体结合的自发参量下转换过程，得到了超高亮度的偏振纠缠光子对光源（如图7），并利用此光源来检验Bell不等式，实验数据是S=2.7007±0.0029，在不到3分钟内获得了对Bell不等式的违反达242个标准偏差。根据此处给出的实验数据和违反的标准偏差数，可判知该实验违反的是CHSH不等式。

 

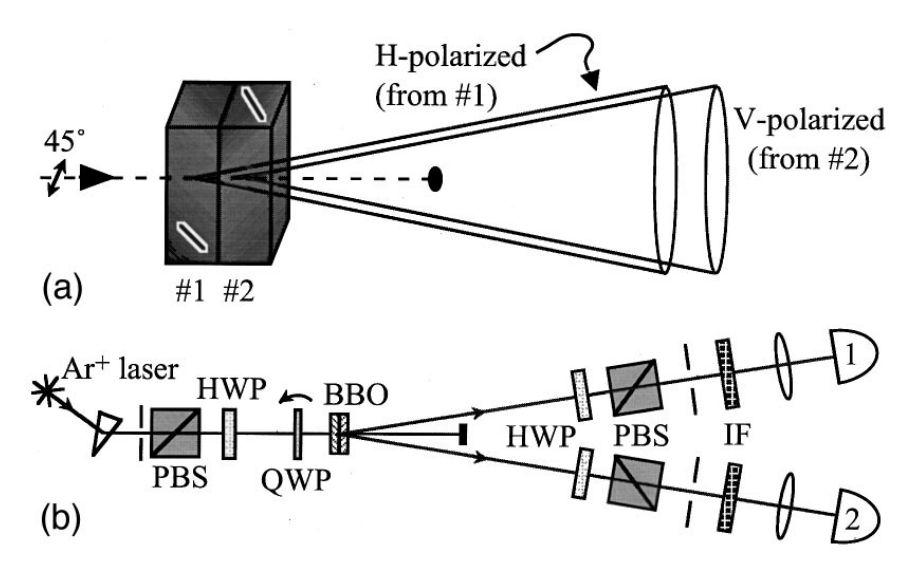
图7.(a)两个相同的下转换晶体中产生偏振纠缠光子的方法，方向相互为90°; (b)实验装置示意图[10]

 

2001年，中国科学技术大学的Yun-feng Huang（黄云峰），Chuan-feng Li（李传锋），Yong-sheng Zhang（张永生）和Guang-can Guo（郭光灿）[11]发表“Experimental test of CHSH inequality for non-maximally entangled states”一文，他们采用两块BBO晶体结合的自发参量下转换产生纠缠光子对，提出了对于非最大纠缠态时对CHSH不等式最大违反的检验方法（如图8），该实验获得数据是S=2.7277±0.0719，以10个标准偏差违反CHSH不等式。本实验是使用非最大纠缠态对Bell不等式进行检验的最早实验之一。

 

图8. 产生非最大纠缠态和测量S值的实验装置示意图[11]

 

2003年，Aspelmeyer，Zeilinger等13位作者[12]在Science杂志发表“Long-Distance Free-Space Distribution of Quantum Entanglement”一文。文中实验使用了由Ⅱ类参量下转换BBO晶体产生的偏振纠缠的光子对，不同于以往的实验，此实验首次不借助于光纤传输，在分离600米的自由空间中完成。以此为基础，在2005年中国科学技术大学Jian-wei Pan（潘建伟）团队等13人[13]实现了纠缠光子在13公里长的自由空间中的分发，这是当时最长的距离。实验表明，两个纠缠光子即使已经穿越噪杂的城市环境（大气背景），所期望的纠缠依然存在。两项试验实验都是对CHSH不等式进行了检验，证明了对Bell不等式的违反。

 

随着贝尔不等式的提出，人们可以在实验上检验量子非局域性。由于实验装置的不完美，绝大多数实验都存在漏洞，其中广受关注的漏洞包括探测效率漏洞和定域性漏洞等。在2015年，科学家们首次在二维纠缠体系中同时关闭了效率漏洞和定域性漏洞，并以此为基础发展出了各种设备无关的量子信息任务。2022年，我科学家也首次实现了无探测漏洞的高维贝尔不等式检验，中国科学技术大学郭光灿院士团队李传锋、柳必恒研究组利用BBO晶体制备纠缠光子，将高维纠缠光子的总体探测效率提升到71.7%[14]，从而实现了无探测漏洞的高维贝尔不等式检验（如图9）。该成果为进一步实现同时关闭探测漏洞和非局域性漏洞的高维贝尔不等式检验及设备无关的高维量子通信过程奠定重要基础。

 

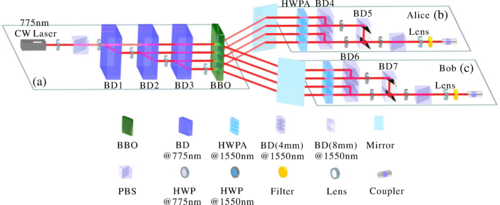
图9.无探测漏洞的高维贝尔不等式实验装置示意图[14]

 

总结与展望

 

时至今日，虽然量子纠缠已被证实，但科学家们仍然在量子力学前进的道路上奋力前行。纵观纠缠光子实验的发展史，许多重要的量子纠缠实验均采用我们福晶科技所发明的BBO晶体，在制备纠缠光子的过程中起到了重要作用，也让我们有机会参与到在这场物理学重大哲学争论中来。

 

科学家们通过BBO晶体设计出更简单、更稳定的纠缠光子实验方案，得到了亮度更高传播更远的纠缠光子，极大促进了这类实验以及对量子力学基础的研究。在量子纠缠实验中，越来越多的科学家选用BBO晶体，也让我们看到了我们的晶体在世界上深远广泛的影响以及更大的潜力和商业价值。未来我们相信，随着量子科学的发展，BBO晶体将会在量子通信、量子密码学、密集编码、隐形传态和量子计算等领域发挥重要作用，BBO晶体也将会拥有更广阔的市场。很荣幸我们的BBO晶体能身处于量子力学快速发展的时代并与之一路同行。

 

 

参考文献

[1]J.S.Bell.On the Einstein-Podolsky-Rosen Paradox [J].Physics,1964(1):195-200.

[2]J.Clauser,M.Horne,A.Shimony,R.Holt.Proposed Experiment to Test Local Hidden-Variable Theories[J].Phys.Rev.Lett.,1969 23(15):880-884.

[3]J.Clauser,M.Home.Experimental Consequences of Objective Local Theories[J].Phys.Rev.D,1974 10(2):526-535.

[4]A.Aspect,J.Dalibard,G.Roger.Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers[J].Phys.Rev.Lett.,1982 49(25):1804-1807.

[5]Y.H.Shih,C.O.Alley.New Type of Einstein-Podolsky-Rosen-Bohm Experiment Using Pairs of Light Quanta Produced by Optical Parametric Down Conversion[J].Phys.Rev.Lett.,1988 61(26):2921-2924.

[6]J.Brendel,E.Mohler,W.Martienssen.Experimental Test of Bell’s Inequality for Energy and Time[J].Europhys.Lett.,1992,20(7):575-580.

[7]T.Kiess,Y.H.Shih,A.Sergienko,C.Alley.Einstein-Podolsky-Rosen-Bohm Experiment Using of Light Quanta Produced by Type-II Parametric Down Conversion[J].Phys.Rev.Lett.,1993 71(24):3893-3897.

[8]P.Kwiat,K.Mattle,H.Weinfurter,A.Zeilinger.New High Intensity Source of Polarization Entangled Photon Pairs[J].Phys.Rev.Lett.,1995 75(24):4337-4341.

[9]G.Weihs,T.Jennewien,C.Simon,H.Weinfurter,A.Zeilinger.Violation of Bell’s Inequality under Strict Einstein Locality Conditions[J].Phys.Rev.Lett.,1998 81(23):5039-5043.

[10]P.Kwiat,E.Waks,A.Whit,I.Appelbaum,P.Eberhard.Uhrabright Source of Polarization Entangled Photons[J].Phys.Rev.A,1999 60(2):R773-R776.

[11]Yun-feng Huang,Chuan-feng Li,You-sheng Zhang,Guang-can Guo.Experimental test of CHSH inequality for non-maximally entangled states[J].Phys.Lett.A,2001 287(5&6):317-320.

[12]M.Aspelmeyer,et al.Long-Distance Free-Space Distribution of Quantum Entanglement[J].Science,2003 301:621-623.

[13]Cheng-zhi Peng,et al.Experimental Free-space Distribution of Entangled Photon Pairs over 13 km:Towards Satellite-Based Global Quantum Communication.[J].Phys.Rev.Lett.,2005 94(15):150501(4).

[14]Xiao-Min Hu,et al.High-Dimensional Bell Test without Detection  Loophole.[J].Phys.Rev.Lett., 129, 060402.

 

如涉及作品内容、版权和其它问题，请在7日内与本平台联系（邮箱：2900646553@qq.com），我们将在第一时间给予处理！